Japanese Temple Geometry
Backgraund Figure is Japanese Traditional Pattern "KAGOME"
FUKAGAWA Hidetoshi & HORIBE Kazunori
 |
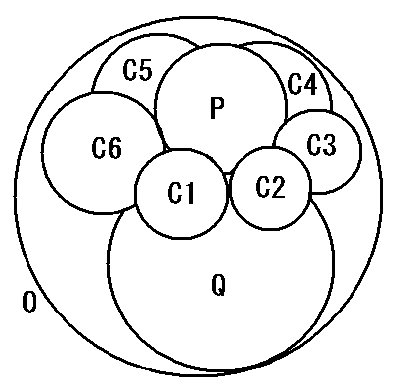
Soddy's Hexlet 球Oに内接しながら、 2球P,Qが外接しているとする。 このとき、球Ci (i=1.2.3.・・・,n)が、 3つの球O,P,Qに外接しながら、 順次外接するならば、 n=6 で、C1とC6は外接する。 Ani. gif file v.0 (219KB) Ani. gif file v.1 (221KB) Ani. gif file v.2 (218KB) Ani. gif file v.3 (693KB) |
 Animation gif file v.4 (686KB) |
 |
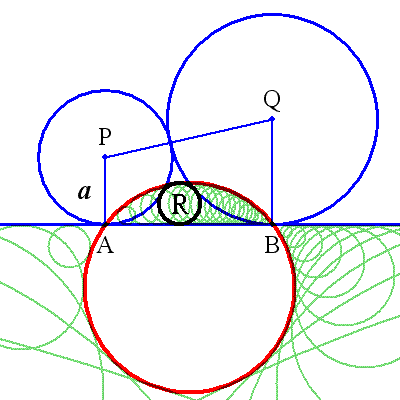
互いに外接し各々が 直線ABに接する2円 P,Qと直線ABに接する 円の包絡線は、 半径{5/8}ABの円である。 宮城県仙台市 釈迦堂天満宮 に掲額された算額から 年代不詳・現存しない GRAPES file 2circle_envelope.gps Function Graphing Software ?? GRAPES ?? |
 Animation gif file(210KB) |
 |
楕円に内接する菱形の内接円は閉形である 出典は、名古屋市中区、大須観音堂に、 天保12年(1841年)に掲額された算額より 深川英俊 ダン・ペドー 共著 「日本の幾何−−−何題解けますか?」 P117−118 例題8.2にあります なお、この問題も 深川先生から直接教えてもらいました。 感謝 (^_^)v です。 上記の本は、面白い問題の宝庫です・・・ね。 GRAPES file oval_rhombus.gps Function Graphing Software ?? GRAPES ?? |  Animation gif file(101KB) Animation gif file Ver.2(82KB) |
 |
円の中心をUとすると、OU=a+b となる。 問題は書名および年記のない平野喜房の写本より 深川英俊 ダン・ペドー 共著 「日本の幾何−−−何題解けますか?」 P93−95 例題6.1にあります なお、以上のことは、 深川先生から直接教えてもらいました。 感謝 (^_^)v です。 GRAPES file oval_circle.gps Function Graphing Software ?? GRAPES ?? | 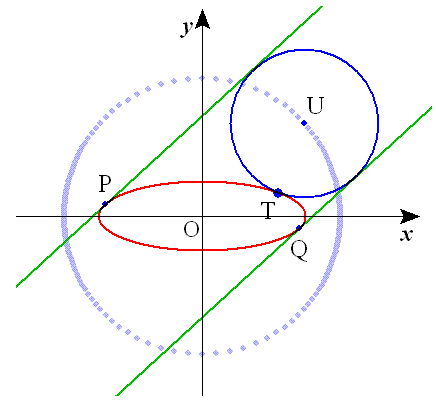 Animation gif file(124KB) |
 |
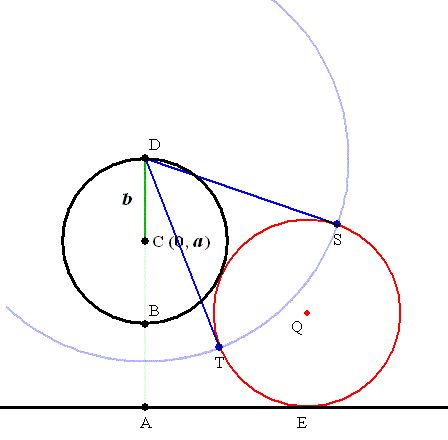
<<注>>算額のアイデアからの問題です 算額そのものにはありません。 定直線Eと定円Cがある。 それらに接する円Qへ、図の点Dから接線DS,DTを引く。 このとき、円Qの位置に依らずに、DS(=DT)は一定である。 GRAPES file oval_circle.gps Function Graphing Software ?? GRAPES ?? |
 Animation gif file(109KB) |
 |
<<注>>算額のアイデアからの問題です 算額そのものにはありません。 円周上の任意の点Pから、直径ABに垂線PTを下ろし、 AT,BTを直径とする円R,Sを描く。 この2円と、PA,PBとの交点をD,Eとすると、 直線DEは、2円R,Sの共通接線である。 GRAPES file 3circ001.gps Function Graphing Software ?? GRAPES ?? |
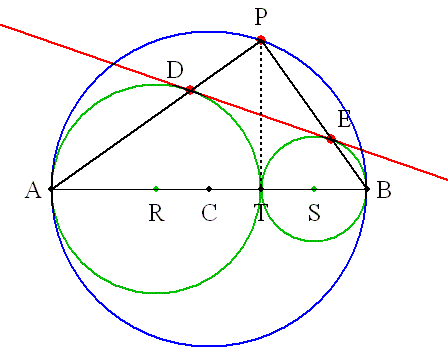 Animation gif file(58KB) |
 |
半円に内接する楕円の短軸を 高さとする台形の対角線は、 長軸の長さと等しい。 TS=PR circle_ellipse.gps Function Graphing Software ?? GRAPES ?? |
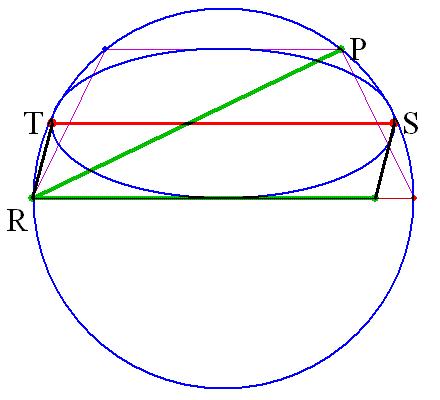 Animation gif file(67KB) |
 |
2点A,Bは2円P,Qの中心線上にあり、それぞれの円の直径の端点(☆)である。 いま、2点A,Bから、それぞれもう一方の円に2本ずつ接線を引く。 接線と円で囲まれた図形(※)に内接する2つの円の半径は常に等しい。 (☆)端点は、2つずつあるが、もっとも遠い2点をA,Bとする。 (※)扇形のようであるが、扇形ではないことに注意。 熱田神宮(名古屋市)にあった算額からの問題です。 ただし、正確には算額は現存しているわけではなく、 算額を書写した、書写本の中にその記述があるそうです。 深川英俊先生に教えて頂いた問題です。 GRAPES file cir_tan2T.gps Function Graphing Software ?? GRAPES ?? |
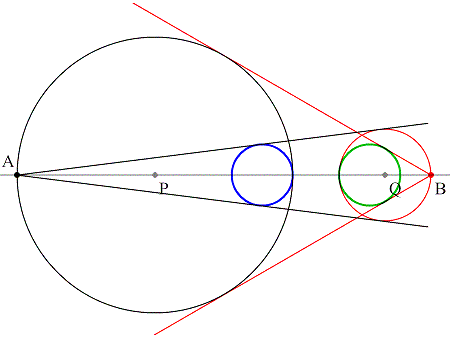 Animation gif file(121KB) |
 |
算額そのものにはありません。 2円の中心P,Qから、互いに2本ずつ接線を引く。 接線と円P,Qの交点を、A,BおよびC,Dとする。 このとき、常に線分ABとCDの長さは等しい。 マシンの能力によって、 動きがギクシャクすることもあります。 GRAPES file cir_tan1T.gps Function Graphing Software ?? GRAPES ?? |
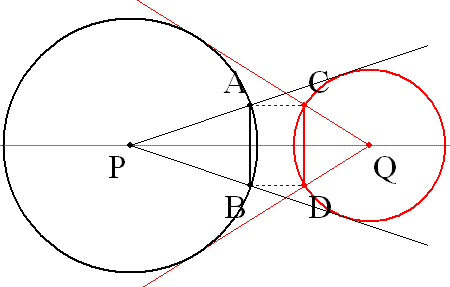 Animation gif file(74KB) |
 |
そのすべてに接する大きな球の半径は、 √5倍である。 PDF file sanpoujojutsu19.pdf 30balls.pdf for30balls.pdf GRAPES file 30balls.gps Function Graphing Software ?? GRAPES ?? |
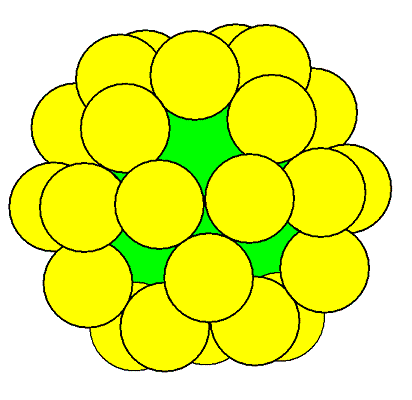 Animation gif file(29KB) 30 balls photo(55KB) |
Function Graphing Software
|

go to top page
 go to Japanese Math |
Go To Japanese Math (English Page) |